The quantum computer was ahead of the classical one in solving a new problem, or rather in testing this solution. Physicists have experimentally implemented a protocol for verifying the solution of a problem that cannot be solved on a classical computer in polynomial time. They showed that a quantum machine requires a thousand times less information to test. The work is published in Nature Communications.
A quantum computer is not stronger and more powerful than a classical computer in any task, we discussed this in more detail in the article " When to expect quantum superiority» . So far, scientists have been able to demonstrate quantum superiority on the problems of random string generation and boson sampling. From an applied point of view, these tasks are not of any value-they show the possibilities of quantum computers and their future as a whole. The demonstration of the solution of more applicable and real problems rests on a small number of qubits of the calculator.
The choice of problems that students learn to solve on quantum computers is not accidental. A quantum computer must cope with tasks that take an unlimited amount of time to solve. Scientists have long faced such problems and have already managed to divide them into complexity classes, depending on how quickly the time to solve the problem increases with an increase in the number of input data. Moreover, the time required to solve the problem is the time required for the fastest algorithm. The uncertainty that lurks in the term "fastest algorithm" (suddenly there is one, but scientists have not yet invented it and found it) gives rise to the well-known problem of equality of classes P and NP. The NP complexity class includes problems whose solution can be verified in polynomial time if additional information is available, and the P class includes problems for which the dependence of the solution time on the dimension of the problem is polynomial. It is believed that quantum algorithms can put an end to this issue.
One of the most popular problems for quantum computers is the problem of the satisfiability of Boolean formulas ( SAT ). It not only belongs to the NP class, but any NP complex problem can be reduced to it (such a subclass of NP complexity is called NP-complete ). The N-SAT problem consists of a set of conditions, each of which in turn consists of N Boolean variables (can take the values 0 or 1). The condition can include both a variable and its negation (NOT). The problem can be solved if you find such a set of variables that the final formula is correct (equal to 1). For example, a 2-SAT task might look like this: (X1 OR X3) AND (NOT X2 OR X1). It turns out that to solve the problem, you need each bracket to be equal to 1. Then it is enough to fix X1 = 1, and X2 and X3 can be any. It is clear that increasing the number of conditions (brackets) complicates the task, as does the number of elements in the bracket.
A team of physicists led by Iordanis Kerenidis were able to show experimentally that a quantum computer is faster at verifying the solution of an NP-complete problem than a classical one and considered all possible real limitations that arise in the experiment. Scientists considered an interesting 2-out-of-4 SAT problem: in each bracket of four variables, at least two must be 1.
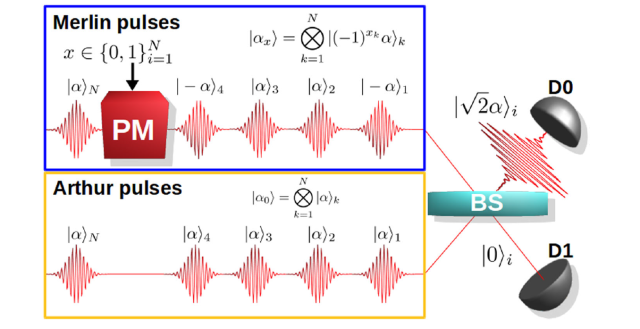
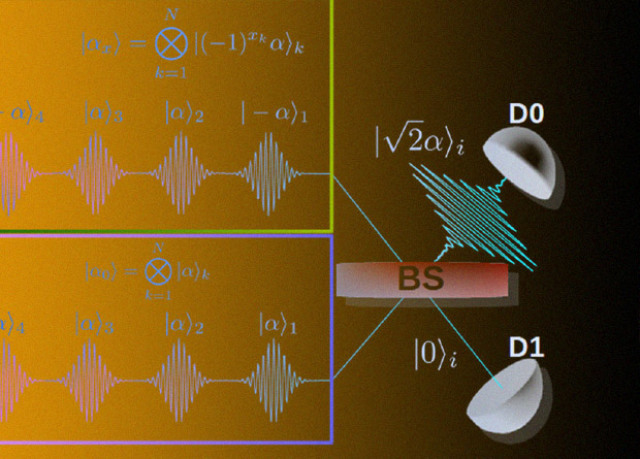
A scheme for checking the solution that Merlin sends. At the same time, Arthur generates a sequence of coherent pulses that interact with Merlin's pulses in turn, and depending on which detector the click is detected, you can understand what state Merlin sent
Image source: Federico Centrone et al. / Nature communications, 2021
In order to implement the verification of the solution, you need two people — in the quantum world, this is Merlin and Arthur. Merlin finds some supposedly correct solution to the problem and sends it to Arthur, who checks this solution for correctness. It is important to note that Merlin and Arthur work under conditions of limited information, meaning Merlin cannot send the entire task. And in the classical world, if Arthur checks for one random condition, then Merlin can change the values of the variables each time, which will distort the check. In the quantum world, Merlin encodes a possible solution to the problem using coherent states and sends it to Arthur. Arthur prepares his set of sequential states with the desired amplitude and time division. The Arthur and Merlin states interfere on the beam splitter and, depending on the phase of the Merlin state, either one or the other detector clicks. Increasing the number of photons in a single pulse increases the probability of detecting the state and makes the circuit more efficient.
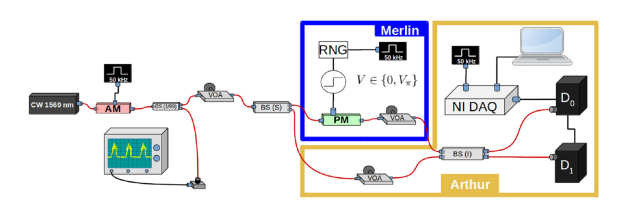
Installation diagram for checking the solution of the feasibility problem
Image source: Federico Centrone et al. / Nature communications, 2021
Two probabilities play an important role in verifying the correctness of a decision: the first one shows how often the verification result confirms this with a really correct decision, and the second one describes the situation when the verifier made the wrong decision for the right one. They try to increase the first (C) and reduce the second (S). The authors managed to get C greater than 0.9 while holding S less than 0.6.
In addition, for an incorrect decision, the number of conditions that were not met is important. Scientists recorded this value at 15 percent, the number of variables they chose was equal to ten thousand. To calculate the real experimental scheme, they took into account the imperfection of the detectors and chose a visibility value of 0.91 (ideally, it is equal to 1). With all these parameters, we investigated and searched for such an optimal number of photons per pulse to demonstrate the advantages of a quantum computer over a classical one. It turned out that the gap between the probability of C and S is close to one in a wide range, and for the experiment, the authors used a value of 1.31. The experiment showed that the quantum computer requires a thousand times fewer bits than the classical one.
The problem of verifying the solution, in contrast to the previous problems for demonstrating the capabilities of quantum computers, takes a step towards real-world applications. Physicists suggest using powerful quantum computers to solve problems, and checking the correctness of solutions is carried out on less powerful machines. They see the quantum Internet as another possible application.
The" iron " in the experiment of scientists was photons, as in the experiment of Chinese physicists, who showed the advantage of a quantum computer in solving the problem of boson sampling. And the very first demonstration of quantum superiority was the work of Google scientists, in which they used a superconductor calculator.
Oksana Borzenkova