量子计算机在解决一个新问题,或者更确切地说在测试这个解决方案方面领先于经典计算机。 物理学家已经通过实验实现了一个协议,用于验证在多项式时间中无法在经典计算机上解决的问题的解决方案。 他们发现,量子机器需要一千倍的信息来测试。 工作 已发布 在 自然通信.
量子计算机并不比任何任务中的经典计算机更强大,更强大,我们在文章中更详细地讨论了这一点 "什么时候期待量子优势» . 到目前为止,科学家们已经能够证明在随机字符串生成和玻色子采样问题上的量子优势。 从应用的角度来看,这些任务没有任何价值-它们显示了量子计算机的可能性以及整个未来。 更适用和实际问题的解决方案的演示取决于计算器的少量量子比特。
学生在量子计算机上学习解决的问题的选择并非偶然。 量子计算机必须应付需要无限时间才能解决的任务。 科学家们长期以来面临着这样的问题,并已经成功地将它们划分成复杂的类,这取决于如何快速地解决问题的时间随着输入数据的数量的增加而增加。 而且,解决问题所需的时间是最快算法所需的时间。 潜伏在术语"最快算法"中的不确定性(突然有一个,但科学家们还没有发明它并发现它)引起了众所周知的类p和NP平等问题。 NP 复杂度类包括的问题,其解可以在多项式时间验证,如果额外的信息是可用的,和 P类 包括求解时间对问题维数的依赖性为多项式的问题。 据认为,量子算法可以杜绝这个问题。
量子计算机最常见的问题之一是布尔公式的可满足性问题 ( SAT ). 它不仅属于NP类,而且任何NP复杂问题都可以减少到它(这样的np复杂度的子类被称为 NP-完成 ). N-SAT问题由一组条件组成,每个条件依次由N个布尔变量组成(可以取值0或1)。 条件可以包括变量及其否定(NOT)。 如果您发现这样一组变量,最终公式是正确的(等于1),则可以解决问题。 例如,2-SAT任务可能如下所示:(X1或X3)和(不是X2或X1)。 事实证明,为了解决这个问题,你需要每个支架等于1。 然后,它足以解决X1=1,X2和X3可以是任何。 很明显,增加条件(括号)的数量会使任务复杂化,括号中的元素数量也是如此。
由Iordanis Kerenidis领导的一组物理学家能够通过实验证明,量子计算机比经典计算机更快地验证NP完整问题的解决方案,并考虑了实验中出现的所有可能的实际限制。 科学家们认为一个有趣的2-out-of-4SAT问题:在四个变量的每个括号中,至少有两个必须是1。
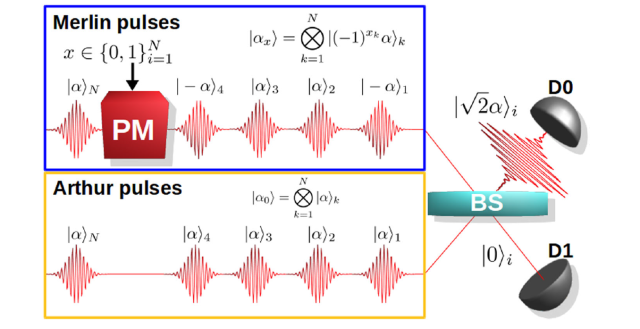
用于检查梅林发送的解决方案的方案。 与此同时,Arthur生成一系列相干脉冲,依次与Merlin的脉冲相互作用,并根据检测到点击的检测器,您可以了解Merlin发送的状态
图片来源:Federico Centrone等。 /自然通讯,2021
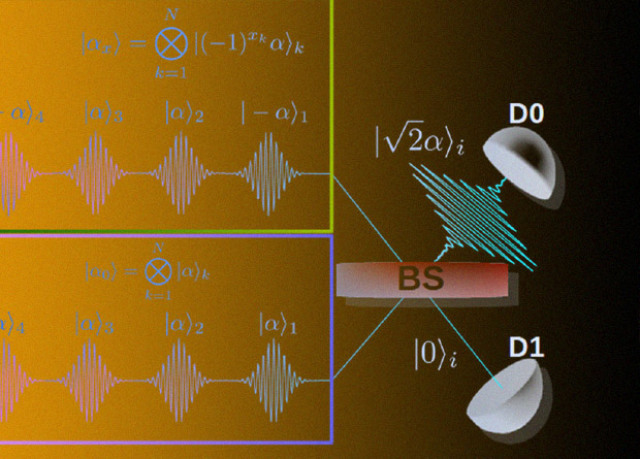
为了实现解决方案的验证,你需要两个人-在量子世界中,这是梅林和亚瑟。 梅林发现一些所谓正确的解决方案的问题,并将其发送给亚瑟,谁检查这个解决方案的正确性。 需要注意的是梅林和亚瑟在信息有限的条件下工作,这意味着梅林无法发送整个任务。 而在古典世界中,如果亚瑟检查一个随机条件,那么梅林每次都可以改变变量的值,这将扭曲检查。 在量子世界中,梅林编码使用问题的可能解决方案 协调一致的国家 发给亚瑟 亚瑟准备他的一套顺序状态与所需的幅度和时间划分。 Arthur和Merlin状态干扰光束分离器,并且根据Merlin状态的相位,一个或另一个检测器咔嗒声。 增加单个脉冲中的光子数量会增加检测状态的概率,并使电路更有效率。
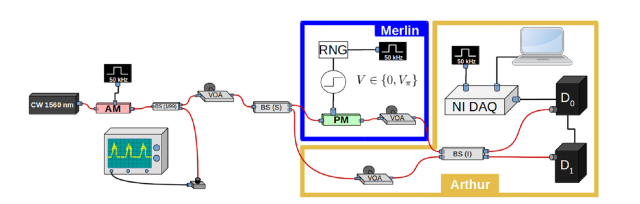
用于检查可行性问题解决方案的安装图
图片来源:Federico Centrone等。 /自然通讯,2021
两个概率在验证决策的正确性方面起着重要作用:第一个概率显示验证结果以真正正确的决策证实这一点的频率,第二个概率描述验证者为正确的决策做出错误决定的情况。 他们试图增加第一个(C)和减少第二个(S)。 作者设法获得C大于0.9,同时保持S小于0.6。
此外,对于不正确的决定,未满足的条件数量非常重要。 科学家在15百分比记录了这个值,他们选择的变量数量等于一万。 为了计算真正的实验方案,他们考虑到探测器的缺陷,并选择了0.91的可见性值(理想情况下,它等于1)。 所有这些参数,我们调查和搜索每脉冲的光子的这种最佳数量,以证明量子计算机优于经典的优势。 原来,c和S的概率之间的差距是接近一个在很宽的范围内,并为实验中,作者使用的值为1.31。 实验表明,量子计算机比经典计算机需要的比特少一千倍。
验证解决方案的问题与以前的量子计算机功能演示问题相反,向现实世界的应用程序迈出了一步。 物理学家建议使用强大的量子计算机来解决问题,并检查解决方案的正确性是在功能较弱的机器上进行的。 他们认为量子互联网是另一种可能的应用。
科学家实验中的"铁"是光子,就像中国物理学家的实验一样 显示 量子计算机在解决玻色子采样问题中的优势。 量子优势的首次展示 是 谷歌科学家的工作,在他们使用的超导体计算器。
Oksana Borzenkova