Виртуальный нейрокомпьютер (НК) «Эмбрион» разработан в СССР под руководством В.Д. Цыганкова (1) с участием академика П.К. Анохина. НК «Эмбрион» представляет собой техническую модель мозга, возбуждение квазинейронной сети в котором создаёт виртуальное когерентное волновое поле (2). Виртуальным квазинейронам соответствуют вероятностные события активации бинарных кодов (точки бифуркации) на определенных тактах дискретного внутреннего времени устройства. При этом, «Эмбрион» представляет собой вариант многомерной ассоциативной кратковременной памяти в виде модели нейрона или сети нейронов кибернетической функциональной системы управления. Функционирование нейронной сети воспроизводит известную в нейрофизиологии Шеррингтоновскую воронку – афферентные входы нейронных сетей конвергируют между собой, объединяясь через общие структуры в эфферентный канал. «Эмбрион» рассматривается как макроквантовый когерентный нейронный компьютер (3).
На сегодня известно несколько модификаций данного нейрокомпьютера для различных приложений: датчик случайных многомерных управляемых импульсных потоков, интерсенсорный перенос «глаз–рука», техническая диагностика неисправностей энергогенератора самолётной электростанции, система нейронного распознавания символов алфавита, нейрокомпьютерная система стабилизации полета летательного аппарата, электронный мозг мобильного робота и др (4).
В связи с биомеханическими особенностями нейрокомпьютера «Эмбрион» на его основе возможно адаптивное биоуправление с кибернетического обратной связью. В частности, биопротезы с бионическим нейросетевым контроллером могут применяться в задачах управления сложными динамическими объектами. Специфика такого нейроуправления обусловлена функционированием искусственной нейронной сети, действующей под управлением нервной системы оператора. Данный вид управления в системе человек-машина использует выраженную нелинейность открытого отображения пространства входных векторов в пространство топологий и динамики виртуальных нейронных сетей.
В соответствии с архитектурой «Эмбриона» (4), двигательные регуляторы манипуляторов управляются реципрокными сжимателями бионической сети мотонейронов. Управляющий сигнал, например, ЭЭГ или мышечная активность оператора, поступает на сенсорную матрицу нейрокомпьютера, которая представляет собой модель проекционной зоны коры головного мозга, находящейся под управлением модели очагов доминанты Ухтомского – блока выдвижения гипотез (4). В результате нейросетевого распознавания входного образа нейрокомпьютером генерируется поток частот, управляющих мотонейронов. Этот поток представляет собой параметры ассоциативной нейронной сети, рефлекторно реагирующей на команды оператора. Для управления можно использовать методы фрактального сжатия сети, измерения спектра частот нейронов, а также аналитические методы. При установлении биологической обратной связи происходит конвергенция и взаимная адаптация искусственных и естественных нейронов в рамках объединенной функциональной системы.
Опыты на кибернетической модели мозга анимата (Цыганков В.Д., Шарифов С.К., Шарифов Н.К. ,2004) показали, что в зависимости от конфигурации параметров блока выдвижения гипотез (4) можно различить различные режимы функционирования управляемого привода, включая его высокую подвижность и почти полную остановку. Эксперименты с очувствленным роботом позволили смоделировать в реальном времени функциональную систему П.К. Анохина (4), рефлекторные акты, обучение, аккомодацию, ассимиляцию, эпилепсию, судороги и другие эффекты высшей нервной деятельности. Фрагменты эксперимента запечатлены на видео (5). Все перечисленные эффекты получены без участия центрального процессора Фон-Неймановской архитектуры и каких-либо программируемых вычислений, используемых в классических нейронных сетях или на обычных ЭВМ с архитектурной Фон-Неймана.
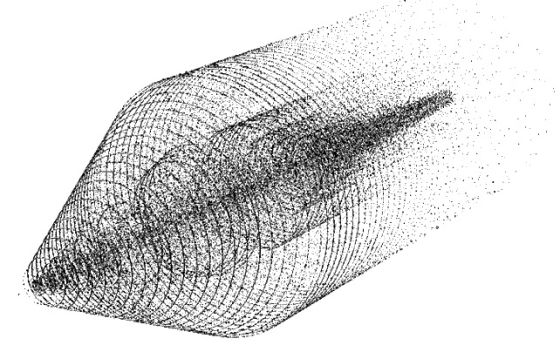
Рассмотрим особенности и закономерности генерации нейронных сетей в нейрокомпьютере «Эмбрион». На рис. 1 изображена предложенная В.Д. Цыганковым интерпретация эволюции состояний нейросети нейрокомпьютера. Процесс генерации нейронной сети начинается из начальной точки сингулярности – входного “инициирующего” нейрона, вероятность активации которого P0(X)=1, X=const, где X – начальное состояние. Каждая концентрическая окружность соответствует обобщенному такту внутреннего счетчика. Состояние нейро-ЭВМ в каждом сечении представлено набором кодов активных нейронов. Точкам внутри каждого сечения соответствуют квазинейроны – вероятностные события активации определенных кодов внутренней памяти. По В.Д.Цыганкову, нейрон расположен тем ближе к центру, чем выше вероятность его активации. По аналогии с квантово-механической волновой функцией, суммарная вероятность активации всех нейронов на каждом обобщенном такте равна единице. На рис. 1 процесс генерации нейронной сети изображен слева направо (из прошлого в будущее) (4).
 |
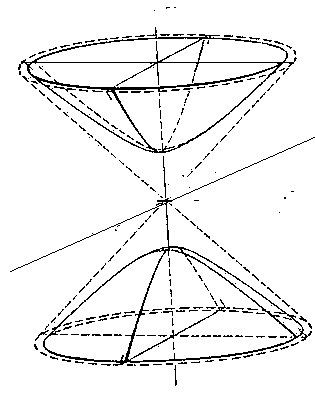| Рисунок 1. Псевдоевклидово пространство Минковского |
| Источник: http://технодоктрина.рф/ |
 |
| Рисунок 1. Причинная упорядоченность виртуального когерентного волнового поля нейрокомпьютера «Эмбрион» в виде эволюции его состояний в марковском пространстве параметров сети (справа). |
| Источник: http://технодоктрина.рф/ |
Причинностный переход в сингулярность отчетливо виден справа в центре по оси в виде хвоста «светового» конуса. При внутреннем времени U=n, где n – разрядность нейрокомпьютера, наблюдается максимальное разнообразие кодов нейронов, а при U> =3n, 99% нейронов концентрируются в аттракторе нейронной сети (вторая сингулярность). Динамика процесса генерации нейронной сети эквивалентна цепной реакции в виде взрыва и последующего медленного остывания и имеет свои особенности (рис.2).
Структурную связь нейрокомпьютера «Эмбрион» с причинно-следственными космологическими моделями можно проследить из аналогии нейросетевого самоорганизующегося динамического процесса со световыми конусами псевдоевклидова пространства Минковского сигнатуры (1, 3). При этом начальную и конечную точки (аттракторы нейронной сети) можно сопоставить с объектами одной из космологических моделей Фридмана – точкам сингулярности. Пример применения теоретико-графового подхода при анализе динамики частично упорядоченных множеств в области "причинностной механики" и квантовой гравитации опубликован в работе Krugly A. L. Stepanian I. V. (6).
 |
| Рисунок 2. Особенности дискретного пространства параметров при подсчете количества бинарных символов в натуральном числовом ряду при одном из вариантов кодирования управляющих сигналов системы управления. Слева – зависимость количества единиц в двоичной записи от ее порядкового номера, справа – зависимость от количества нулей в двоичной записи от ее порядкового номера. |
| Источник: http://технодоктрина.рф/ |
Нелинейная динамика нейронной сети в виде виртуального стохастического процесса порождается и «экстренно мобилизуется» (по П.К.Анохину) в реальном времени в ответ на внешний стимул. Эта динамика достаточно точно приближается к феномену сознания как к форме «опережающего отражения действительности».
Нами были проанализированы биомеханические аспекты и перспективы медико-социальной реабилитации для восстановления утраченных двигательных функций человека: нейрокибернетический подход был перенесен на нарушения здоровья для их профилактики на примере медико-социальной двигательной реабилитации и нейропротезирования. Показана перспективность данного подхода для работников, пострадавших от несчастных случаев и профзаболеваний. Биопротезы с бионическим нейросетевым контроллером могут применяться при управлении сложными объектами. Разработка также актуальна для детей с врожденными аномалиями опорно-двигательного аппарата.
Авторы: Степанян И.В., Плешаков К.В. - Институт машиноведения РАН, Москва
Список литературы:
- Бодякин В.И., Степанян И.В., Цыганков В.Д. Квантовые вычисления на искусственных коллективных нейронных структурах // Нейрокомпьютеры: разработка, применение. – М., 2013. – № 7. – C. 24-31
- Бодякин В.И., Степанян И.В., Цыганков В.Д. Квантовые вычисления на искусственных коллективных нейронных структурах // Нейрокомпьютеры: разработка, применение. – М., 2013. – № 7. – C. 24-31. ; Цыганков В.Д. Квантовые вычисления на нейрокомпьютере. Нейрочип и его работа. LAP LAMPERT Academic Publishing, 2012. ; Цыганков В.Д. Нейрокомпьютер и его применение. - М.: Сол Систем, 1993.
- Цыганков В.Д. Квантовые вычисления на нейрокомпьютере. Нейрочип и его работа. LAP LAMPERT Academic Publishing, 2012.
- Анохин П.К. Биология и нейрофизиология условного рефлекса. - М.: Наука, 1968
- quantum neural networks (Видео-ролик).
- Krugly A. L. Stepanian I. V. An example of the stochastic dynamics of a causal set // Foundations of Probability and Physics – 6, Växjö-Kalmar, Sweden, 14-16 June 2011, AIP Conference Proceedings, V. 1424, edited by Mauro D’Ariano, Shao-Ming Fei, Emmanuel Haven, Beatrix Hiesmayr, Gregg Jaeger, Andrei Khrennikov, and Jan-Åke Larsson. 2012. – P. 206 -210 (arXiv: 1111.5474 [gr-qc]).
