Для анализа и прогноза рационального использования ресурсов, например, неисчерпаемых природных ресурсов, по большому счёту могут быть использованы два подхода. Первый из них – статистический анализ ретроспективных данных о состоянии и использовании ресурсов, на основе которого можно прогнозировать будущие показатели. Второй – математическое моделирование процесса использования ресурса, что может также позволить делать прогнозы относительно состояния ресурсной базы в будущем.
Существующие споры о преимуществах и недостатках обоих подходов не будут рассмотрены здесь, но внимание будет уделено возможностям, которые даёт математическое моделирование в рационализации использования, а, следовательно, в сбережении ресурсов на примере неисчерпаемых природных ресурсов.
Математические модели, описывающие использование природных ресурсов, могут быть разделены на следующие категории.
- Модели, описывающие использование невозобновимых природных ресурсов.
- Модели, описывающие использование возобновимых природных ресурсов.
- Модели, в которых предполагается, что развитие технологий происходит достаточно быстро для преодоления дефицита природных ресурсов.
- Модели, в которых флуктуации экономического роста объясняются динамикой (природных) ресурсов.
Модели невозобновимых природных ресурсов не представляют большого интереса на сегодняшний день, поскольку оптимальная траектория для использования ресурсов такого типа более или менее определена, и многие исследователи согласны с этой траекторией.
На сегодняшний день наибольший интерес представляют модели возобновимых природных ресурсов, поскольку они во многом определяют устойчивость развития экономики и общества. Наиболее известными и популярными моделями для описания динамики возобновимых природных ресурсов, которые используются в экономике природопользования, являются система уравнений Хищник-жертва Лотки и Вольтерры, а также модель логистического роста или, как его ещё называют, уравнение Ферхюльста (Verhulst).
Говоря об этих моделях, приходится констатировать, что для большинства специалистов не математиков эти модели являются сложными для понимания уравнениями, которые эксплуатируют некоторые математические законы, пытающиеся объяснить реальность. Студенты экологи и биологи, природопользователи и географы изучают эти уравнения как что-то обязательное, но совсем не нужное для использования в своей профессиональной деятельности. Такая ситуация нуждается в коренном изменении.
Попытаемся рассмотреть на простом примере, что можно увидеть с помощью математического моделирования одного из процессов, происходящих в природе.
Выше уже было упомянуто уравнение Ферхюльста, или логистического роста. Это уравнение часто используют для описания роста какой-либо популяции. Стоит отметить, что данное уравнение является одним из самых популярных в моделировании процессов роста в окружающей среде, особенно если этот рост связан с использованием невозобновимых природных ресурсов.
Итак, уравнение Ферхюльста часто представляют таким образом:
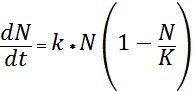 |
| Источник: http://технодоктрина.рф/ |
Учитывая, что представленное выражение является уравнением, необходимо отметить его одну важнейшую характеристику: это дифференциальное уравнение. Особенностью дифференциального уравнения является то, что его решение – это не число. Решение дифференциального уравнения – это функция.
Важным остаётся вопрос: что видят в этом выражении профессионалы в нематематических областях? Вероятнее всего они не станут даже с ним разбираться. Для большинства людей, которые являются профессионалами в своих областях, данное выражение не сообщит никакой конкретной информации. При этом следует учитывать, что приведённое математическое выражение, то есть уравнение Ферхюльста, описывает биологический процесс, а именно динамику популяции в условиях наличия ограничений среды. В отдельных случаях наше уравнение ничего не сообщит даже биологу.
С другой стороны, выразимся так. Скорость роста популяции зависит от размера популяции, коэффициента роста (средней рождаемости, удельной рождаемости) и ёмкости среды. Ёмкость среды не изменяется. На рост популяции влияют такие факторы как: смертность, ёмкость среды, «скученность» особей. Очевидно, что при небольшой плотности популяция растёт низкими темпами, при слишком высокой плотности, учитывая наличие ёмкости среды, популяция также не может расти быстро. Следовательно, популяция должна расти максимальными темпами, когда особей достаточно много, но не настолько, чтобы мешать друг другу.
Такая словесная модель роста популяции будет понятна практически любому человеку, даже не специалисту, который здраво мыслит и может себе представить некоторые процессы, не слишком тесно вплетённые в его жизнь.
Здесь возникает несколько вопросов.
- Описывают ли две модели – словесная и математическая – одно и то же?
- Если ответ на первый вопрос положительный, то для чего нужна математическая модель, которая практически никому не понятна, если есть словесная, которая понятна даже не специалисту?
Если отбросить некоторые детали, то ответ на первый вопрос будет положительным. Следовательно, необходим ответ на второй вопрос.
Ответ на второй вопрос не может быть односложным.
В первую очередь необходимо отметить, что здесь понадобятся детали, которые мы опустили, отвечая на первый вопрос. Эти детали относятся к точности описания одного и того же процесса двумя разными моделями. Словесная модель даёт лишь общее представление о процессе роста популяции. Математическая позволяет дать ответы на конкретные вопросы, разрешить которые вторая модель не может. Например: при каком условии темп роста популяции будет максимальным? Человек, владеющий математическим аппаратом, ответит так: при K/2.
Кроме этого вопроса уравнение Ферхюльста может помочь дать ответ на вопрос о том, каким будет размер популяции в конкретный момент времени. Нужно ли ради этого преодолевать сложность понимания математических выражений, особенно дифференциальных и интегральных? Безусловно, нужно, поскольку системы таких уравнений способны дать определённые чёткие ответы, часто необходимые для принятия обоснованных и верных управленческих решений.
Следовательно, требуется «расшифровать» уравнение.
Итак, приведём уравнение ещё раз.
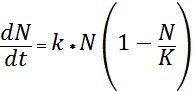 |
| Источник: http://технодоктрина.рф/ |
где:
- k – коэффициент роста популяции;
- N – численность популяции;
- K – ёмкость среды.
Левая часть уравнения DN/Dt говорит о том, что это дифференциальное уравнение. Она показывает, что автор уравнения интересуется, каков будет прирост численности популяции при минимальном, бесконечно малом изменении времени t. А если изменение времени бесконечно малое, то и прирост будет также бесконечно малым. И автор уравнения тут же даёт ответ на это вопрос: это правая часть уравнения, вот чему будет равен прирост. Допустим, мы знаем, что коэффициент роста популяции k равен 0,1; численность популяции N равна 3, а ёмкость среды равна 10. В этом случае прирост в момент времени t (для которого справедливы все названные показатели) dN будет равен 0,21.
Если при прочих равных условиях изменится численность популяции и составит 5, то прирост dN будет равен 0,25. При численности популяции N , равной 7, прирост dN снова составит 0,21. Очевидно, что при нулевой численности популяции N прирост dN тоже будет равен нулю, а при N = K прирост dN будет снова равен нулю.
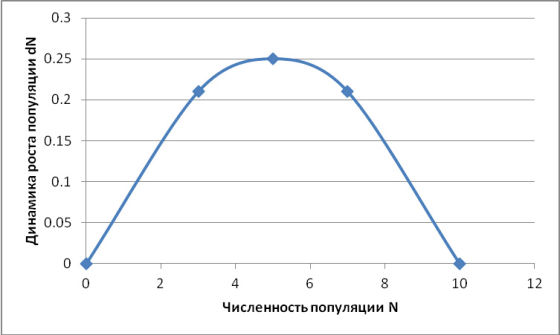 |
| Рис. 1. Зависимость динамики роста популяции от её численности. |
| Источник: http://технодоктрина.рф/ |
С одной стороны мы можем увидеть, что действительно, максимальная скорость роста популяции достигается тогда, когда N = K/2. Мы действительно видим, что если численность популяции близка к нулю или к емкости среды K, то темп роста очень низкий.
С другой стороны, такой подход к анализу модели Ферхюльста в натуральных условиях использовать практически невозможно. Во-первых, это связано с тем, что точно назвать уровень ёмкости среды сложно; во-вторых, коэффициент прироста популяции может быть зависим от времени; в-третьих, чтобы так решать подобные уравнения необходимо обладать достоверными эмпирическими данными об объекте исследования, а в этом случае ценность такой математической модели стремится к нулю.
Поэтому подобные уравнения более целесообразно решать аналитическим способом, чтобы можно было получить, в нашем случае, уравнение зависимости численности популяции от влияющих на неё факторов.
А это важно как для получения научных выводов, так и для принятия управленческих решений. Так, в 1998 г. Дэниел Паули с коллегами в журнале Наука (Science) публикует революционную статью об обеднении трофических цепочек в морях (1). Причиной такого обеднения исследователи назвали перевылов рыбных ресурсов. Они назвали это явление «перевылов морских трофических связей». Суть этого явления заключается в том, что рыбаки сначала вылавливают хищников первого порядка, затем, когда их популяция сокращается настолько, что их особи перестают попадаться в сети, промысловики начинают вылавливать хищников более низкого порядка и так далее. Доказать это удалось с помощью анализа подробных статистических данных. Однако в 2012 г. Кристофер и Джеймс Вилен публикуют статью о том, что выводы, сделанные группой Дэниела Паули, ошибочны, а доказано это было с помощью математической модели (2).
Приведённый элементарный анализ, а также пример из литературы позволяют сделать довольно важные выводы.
- Математические модели могут быть использованы при исследовании естественных процессов, когда отсутствует достаточное количество информации.
- Овладение навыками математического анализа и применение их на практике лицами, принимающими решения, позволит существенно повысить уровень эффективности управленческих решений, поскольку математические модели в отличие от словесных повышают точность описания процессов и явлений.
- Учитывая современный уровень владения навыками математического анализа и моделирования не профессиональными математиками, необходимо разрабатывать и вводить в вузах предметы по математическому моделированию в разных предметных областях.
Автор: Золотарёв Д.В. - канд. экон. наук, ст. науч. сотр. Российского научно-исследовательского института экономики, политики и права в научно-технической сфере
Список литературы:
- Pauly D., Christensen V., Dalsgaard J., Froese R., Torres Fr. Jr. Fishing Down Marine Food Webs // Science. 1998. Vol. 279, №5352, 6 February. – P. 860–863
- Wilen Ch.D., Wilen J.E. Fishing down the food chain revisited: Modeling exploited trophic systems // Ecological Economics. 2012. – Vol. 79, July. – P. 80–88.


