Конкретные результаты инвестиционной и инновационной деятельности в современной России не всегда соответствуют ожиданиям по целому ряду причин, в том числе в связи с недооценкой или прямым игнорированием значимости управления инновационно-инвестиционными процессами, в частности, со стороны государства как основного экономического субъекта.
В то же время в результате ускорения развития и усложнения социально-экономических систем в разных странах мира приходит понимание того, что сложившиеся традиционные формы и методы управления не могут справиться со стремительно нарастающими проблемами, кризисными ситуациями и требуют значительной корректировки и обновления. В современном быстроменяющемся мире методы и формы управления также должны обновляться в направлении большей гибкости, большей адаптивности, повышения способности своевременно решать задачи регулирования инвестиционных потоков для достижения поставленных целей технологического развития на макро- и мезоуровнях.
Новые возможности в совершенствовании инновационно-инвестиционной политики и управления открываются современными подходами, основанными на системном анализе и теории самоорганизующихся систем (синергетике). Предлагаемая синергетическая концепция управления инновационными процессами и сопряжёнными с ними инвестиционными потоками базируется на изучении, анализе и моделировании свойств и состояний переходных инновационно-инвестиционных процессов и обновляемых технологических систем. Действия методом проб и ошибок, попытки управлять сложными переходными инновационными процессами и обновляемыми системами, не зная и/или не учитывая их свойств и не вполне понимая, в каком состоянии они находятся, не позволяют принимать эффективные управленческие решения и стабильно получать желаемые результаты.
Сложные процессы, связанные с технологическим развитием и происходящие в ходе разработки и применения инновационных технологий, видов продукции, услуг и бизнес-моделей, носят ярко выраженный нелинейный характер и сопровождаются необратимыми изменениями. Научно обоснованное управление, прогнозирование и планирование инновационных процессов должны, по нашему мнению, опираться на современные математические модели и методы нелинейной динамики и синергетики. Ряд исследователей (Д Сахал, А. Грюблер, М. Хироока и др.) ранее использовали подобные модели и методы для анализа инновационных процессов. В настоящей работе изучение, анализ и моделирование свойств инновационно-инвестиционных процессов основывается на использовании информационно-энтропийного и мультифрактального подходов, а также вейвлетного анализа, что позволяет глубже понять природу динамики, в том числе цикличности, технико-экономического развития инновационных систем на основе универсальных закономерностей самоорганизации и самоподобия.
Рассмотрим инновационно-инвестиционный процесс развития открытой технологической системы. Такие системы в процессе своего обновления развиваются как открытые диссипативные устойчиво неравновесные системы, способные к самоорганизации (1). Наличие материального, энергетического и информационного потоков (в качестве которых выступают потоки инвестиций, патентной информации, кадров, оборудования и т.д.) от внешних источников к системе и их диссипация являются предпосылками активности обновляемой системы. Рассматриваемые самоорганизующиеся системы включают и профессиональные сообщества, а с психологических позиций сюда целесообразно добавить поток «мотивационной энергии», угасание которого приводит к снижению темпов роста научных знаний, истощению потока инноваций и постепенному разрушению интеллектуальной структуры, что подчёркивает диссипативный характер инновационных систем. Гомеостатические свойства профессионального сообщества определяются такими факторами, как научные школы и исторические традиции, стабильная система образования и классические учебники, которые обеспечивают преемственность и устойчивое развитие науки, техники и технологий. Эта модель открытой активной обновляемой системы вполне соответствует концепции открытых инноваций (2).
Важнейшей функцией состояния системы является энтропия. В открытых системах изменение энтропии можно разделить на сумму двух составляющих: поток энтропии, зависящий от процессов обмена с окружающей средой, и производство энтропии, обусловленное необратимыми процессами внутри самой системы (3). Определённые стадии временной эволюции системы могут происходить при общем понижении энтропии. В соответствии с традиционной интерпретацией энтропии, как меры неупорядоченности системы, это означает, что в ходе эволюции разупорядоченность уменьшается за счёт оттока энтропии, происходит самоорганизация, система эволюционирует к более сложной структуре. При этом могут возникать новые типы диссипативных структур, углубляться иерархия внутри системы и дифференциация подсистем, меняться структура и сложность. В устойчиво неравновесном состоянии положительное производство энтропии внутри системы компенсируется отрицательным потоком энтропии, т.е. притоком информации извне системы или с других иерархических уровней системы (4).
Отличительной особенностью инновационно-инвестиционных процессов является то, что они сопровождаются необратимыми изменениями. Все реальные процессы в той или иной степени необратимы и неравновесны. Источником развития открытой системы является асимметрия потоков вещества, энергии и информации, т.е. наличие градиентов этих величин. В качестве критического элемента обновляемой системы рассмотрена локальная зона повышенного градиента определяющего параметра, лимитирующего режим работы всей обновляемой системы. Для анализа поведения такого критического элемента системы использована модель бистабильного элемента, обладающего двумя устойчивыми состояниями – старым и новым, в каждом из которых он может находиться достаточно долго. Внешние воздействия могут приводить к переходу критического элемента из одного состояния в другое. Чтобы вызвать этот переход, интенсивность воздействия должна превысить некоторый пороговый уровень. В зависимости от соотношения вероятностей P0 и P1 нахождения критического элемента в старом и новом состояниях соответственно, нами рассмотрены три характерных режима существования обновляемой системы: старый (P0 > P1), переходный (P0 = P1) и новый (P0 < P1).
Для анализа эволюции обновляемой системы нами исследована динамика информационной энтропии, которая является мерой неопределённости существования системы, и равна количеству информации по Шеннону, необходимому для снятия этой неопределённости (5):
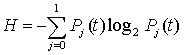 (1) (1) |
| Источник: http://технодоктрина.рф/ |
Иногда удобнее использовать безразмерную относительную энтропийную функцию в виде H/Hmax , где Hmax – максимальное значение информационной энтропии. При этом минимальное значение H/Hmax = 0 соответствует вырождению стохастической системы в жёсткую детерминированную. Достижение максимального значения H/Hmax = 1 в открытой самоорганизующейся системе соответствует точке бифуркации, в которой происходит разрушение исчерпавшей свои диссипативные способности структуры, и начинается этап формирования новой структуры на ином иерархическом уровне. Эта точка соответствует качественному скачку, т.е. переходу обновляемой системы на новый уровень развития.
Аналитическая зависимость для описания динамики потока информационной энтропии H(t) во времени t получена нами в виде (6):
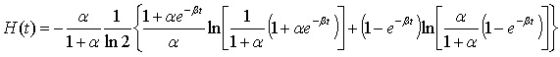 (2) (2) |
| Источник: http://технодоктрина.рф/ |
где
- α = ν / μ - параметр режима существования обновляемой системы;
- β = ν = μ, ν, μ – интенсивности переходов критического элемента обновляемой системы соответственно из старого состояния в новое и обратно.
Выполнен также анализ потока информационной энтропии и скорости его изменения, как отклика обновляемой системы на изменение условий существования. На рис. 1 показаны графики изменения потока информационной энтропии H(t) и его скорости dH/dt для случая, когда в условный момент времени t = 1,4 на систему оказывается воздействие, приводящее к переходу от старого (α<1) к новому (α*>1) режиму существования, т.е. к её инновации. Анализ полученных нами зависимостей показал, что обновляемая система реагирует на сильное воздействие, приводящее к новому режиму существования, резким возрастанием потока информационной энтропии от достигнутого в предшествующих условиях стационарного уровня НST до максимума Н*max = 1 в критической точке t*b. При этом скорость dН*/dt* приращения потока энтропии резко падает до нуля, становится отрицательной, проходит минимум и стремится к нулю, когда обновляемая система входит в новое стационарное состояние. После прохождения критической точки t*b поток информационной энтропии уменьшается и стабилизируется на новом стационарном уровне H*ST, соответствующем масштабу инновации.
В критической точке, соответствующей моменту времени t*b, дисперсия Dx определяющего параметра X обновляемой системы также достигает максимума. В этот момент система характеризуется наибольшей разупорядоченностью, хаотичностью, когда случайные флуктуации проявляются на макроскопическом уровне. Критическая точка t*b, являющаяся стохастическим аналогом точки бифуркации, ассоциируется с процессом самоорганизации, т.е. разрушением старой диссипативной структуры, исчерпавшей свои возможности, и появлением новой структуры, соответствующей изменившимся в результате инновации условиям существования, переходу обновлённой системы на новый уровень развития. Открытая система адаптируется к новым условиям путём совершенствования структуры и возвращается в стационарное состояние благодаря оттоку энтропии и притоку информации извне или с других иерархических уровней обновляемой системы. Полученные нами математические выражения позволяют прогнозировать момент наступления критического состояния обновляемой системы, когда целесообразно принять меры, способствующие скорейшей адаптации обновляемой системы к новым условиям.
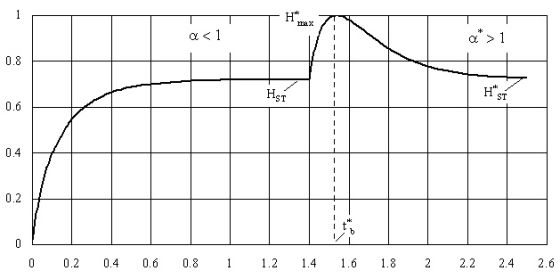 |
| Рис. 1. Динамика изменения потока информационной энтропии H(t) и его скорости dH/dt |
| Источник: http://технодоктрина.рф/ |
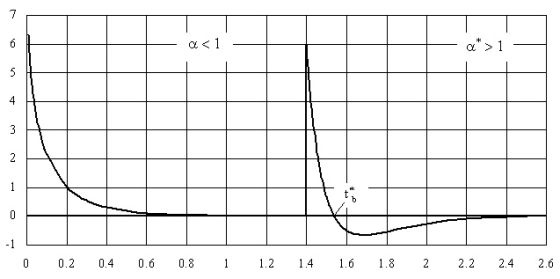 |
| Рис. 1. Динамика изменения потока информационной энтропии H(t) в случае инновации системы (α<1; α*>1). |
| Источник: http://технодоктрина.рф/ |
Потенциальные возможности, возникающие в момент бифуркации, притягивают развитие обновляемой системы, она самоорганизуется, совершенствует свою структуру, переходит на качественно новый уровень развития. Отсюда вытекает представление о том, что технологическое развитие определяется не начальными условиями и «тяжёлым наследием прошлого», а будущими возможными состояниями, т.е. аттракторами технологического развития, к которым обновляемая технологическая система стремится после бифуркации. В этой связи под аттрактором в настоящей работе (по аналогии с работой (7) понималось относительно устойчивое состояние обновляемой системы, притягивающее к себе множество траекторий технологического развития, потенциально возможных после прохождения системой критической точки бифуркации.
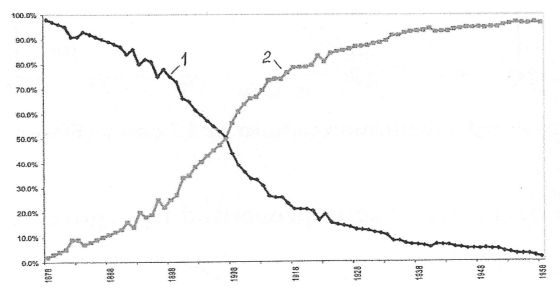
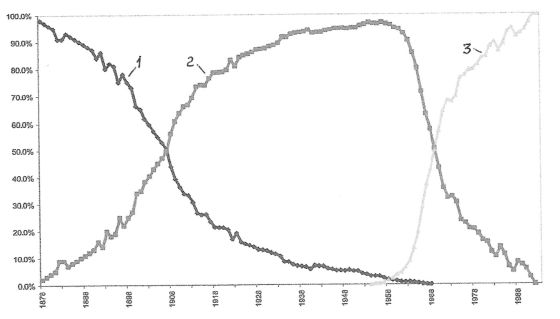
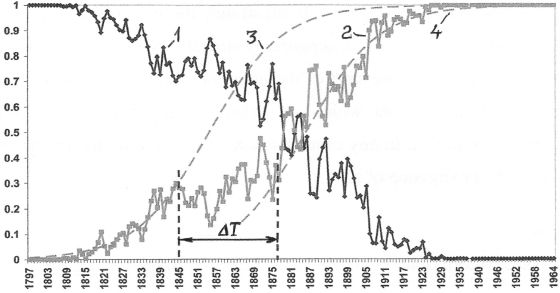
Проанализированы девять типовых траекторий приближения обновляемой технологической системы к аттракторам технологического развития, некоторые из которых («Основной случай», «Последовательность» и «Парусник») показаны на рис. 2–4. На рис. 4 линией 3 нанесена ожидаемая траектория в виде классической логистической кривой, соответствующей модели Фишера-Прая за время с 1797 по 1845 гг., а линией 4 – траектория, построенная с учётом 31-летней задержки T замещения пароходами парусников с 1845 до 1870-х гг., вызванной появлением быстроходных океанских парусных судов (клиперов).
Множество виртуальных траекторий (рис. 5) технологического развития за период времени T отражает классические взгляды на технологические изменения, проявляющиеся во времени в виде последовательной смены поколений технологий с учётом типовых моделей их замещения. Переход с одной виртуальной траектории на другую связан с прохождением критической точки, которая является стохастическим аналогом точки бифуркации (8).
Такая бифуркация в зависимости от условий может привести обновляемую систему к новому стационарному состоянию, как в случае бинарного или последовательного замещения технологий (рис. 2 и 3), либо к довольно длительным колебаниям обновляемой системы между двумя почти равновероятными состояниями, соответствующими преобладанию той или иной из множества конкурирующих технологий, как в типовом примере «Парусник» (рис. 4).
Выявлена зависимость режима существования обновляемой системы и времени прохождения системой точки бифуркации от функции распределения случайного процесса внешних воздействий на систему, её входных потоков, например, инвестиционных и информационных потоков. Так, на рис. 6 приведена зависимость параметра режима существования обновляемой системы при изменении параметров (среднего значения Хm и среднеквадратического отклонения Sx) нормального (Гауссовского) случайного процесса на входе обновляемой системы. Аналогичные зависимости получены также для других вариантов внешних воздействий на входе обновляемой системы. Целенаправленно изменяя параметры входных потоков (материального, энергетического и информационного), в качестве которых выступают потоки инвестиций, патентной информации, кадров, оборудования и т.д. от внешних источников к системе, мы имеем возможность оказывать влияние на время прохождения обновляемой системой критической точки t*b бифуркации. Мы не можем точно предсказать, по какому пути пойдёт развитие обновляемой системы после прохождения точки бифуркации. Однако мы можем предсказать время нахождения системы в этом крайне неопределённом состоянии, характеризуемом наиболее высокими рисками, когда целесообразно предпринять меры, способствующие скорейшему прохождению обновляемой системы через критическую точку и успешной адаптации системы к новому состоянию. Мы можем создать наиболее благоприятные условия для успешного прохождения обновляемой системой точки бифуркации в желаемом направлении, а также предпринять все возможные меры, чтобы направить обновляемую систему по желаемому благоприятному пути развития.
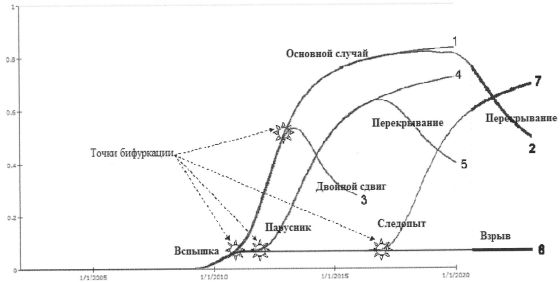 |
| Рис. 5. Множество виртуальных траекторий технологического развития за период времени T и точки бифуркаций на них |
| Источник: http://технодоктрина.рф/ |
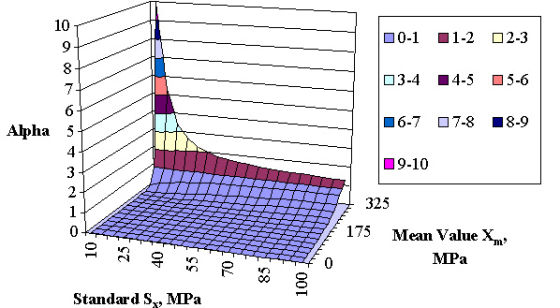 |
| Рис. 6. Изменение параметра режима существования в зависимости от среднего значения Хm и стандарта Sx случайного процесса на входе обновляемой системы. |
| Источник: http://технодоктрина.рф/ |
На рис. 7 показана эволюционная кривая изменения потока информационной энтропии в обновляемой системе при реализации последовательности инноваций, включающая три уровня иерархии и четыре временных интервала. На первом интервале времени критический элемент обновляемой системы существует в старом режиме. В связи с этим поток информационной энтропии за время переходного процесса стабилизируется на уровне НСТ, соответствующем этому режиму, без прохождения точки бифуркации. Через промежуток времени t*b после перехода в новый режим существования (точка 1) обновляемая система проходит точку бифуркации, связанную с разрушением диссипативной структуры первого иерархического уровня (первого цикла). Претерпев скачок развития и выйдя на второй уровень иерархии (второй цикл), обновляемая система выходит на эволюционный этап развития, в течение которого происходит сравнительно медленная стабилизация потока информационной энтропии за счёт насыщения информацией до уровня I=1-H*СТ, соответствующего новому режиму существования самоорганизующейся обновляемой системы. Дальнейший ход временной эволюции обновляемой системы виден из графика (рис. 7). После успешного прохождения точек бифуркации В1 и В2 энтропия по мере притока информации убывает, что означает соответствующее возрастание уровня организации обновляемой системы в процессе её инновационного развития. На каждом иерархическом уровне эволюции – цикле инновационного развития системы в конце процесса самоорганизации, когда «архитектура» обновляемой системы в основном определилась и наступает насыщение информацией, энтропийная кривая постепенно выпрямляется, отображая переход системы в эволюционную стадию своего инновационного развития.
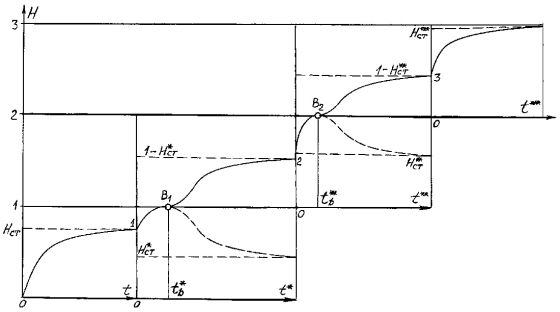 |
| Рис. 7. Эволюционная кривая изменения потока информационной энтропии H(t) во времени в процессе инновационного развития системы |
| Источник: http://технодоктрина.рф/ |
Возрастание степени организации любой системы имеет свой предел, область насыщения, определяемые ограниченными возможностями накопления информации в данной структуре на данном иерархическом уровне – цикле развития обновляемой системы. Каждый переход обновляемой системы на другой иерархический уровень – новый цикл развития неизбежно проходит через критическую точку, являющуюся стохастическим аналогом точки бифуркации. Перевод графиков, показанных на рис. 7, из декартовой в полярную или цилиндрическую систему координат позволяет представить их в виде спиралей технологического развития. Это делает инновационные циклы развития обновляемой системы с чередованием эволюционных и революционных периодов, разделённых точками бифуркации, ещё более наглядными. При этом спирали технологического развития могут раскручиваться или скручиваться в зависимости от того, по какому пути развития следует обновляемая система после каждой точки бифуркации. Полученные математические выражения позволяют прогнозировать момент tb наступления критического состояния обновляемой системы в точке бифуркации и своевременно принять меры по повышению адаптационной способности системы и ускорению её приспособления к новым условиям существования.
Проведённый анализ изменения статистических характеристик (математического ожидания, дисперсии и др.) определяющего параметра системы в новом масштабе времени (после инновации) свидетельствует, что на основе применения информационно-энтропийного критерия выявляются признаки, позволяющие делать выводы о завершении этапа адаптации и о приспособлении обновленной системы к новым условиям существования.
На основе разработанной математической модели получена количественная картина временной эволюции системы, вызванной нововведениями, которая полностью согласуется с представлениями синергетики о качественных процессах самоорганизации неравновесных диссипативных систем. Предложенная модель и полученные математические зависимости позволяют на единой основе описать траекторию технологического развития системы, включая прохождение последовательности точек бифуркации (скачков технологического развития) и эволюционных стадий технологического развития на каждом иерархическом уровне. Переход на новый уровень развития идёт от беспорядка к порядку, через явления неустойчивости в точках бифуркации, где перед обновляемой системой открывается возможность перехода к одному из нескольких аттракторов технологического развития.
В этой связи ставится вопрос о целесообразности учёта и осмысленного анализа аттракторов и точек бифуркации на траекториях технологического развития. Возможность прогнозирования времени наступления точек бифуркации позволяет принимать эффективные управленческие решения и получать желаемые результаты в технологическом развитии страны. В перспективе представляется целесообразным и возможным (при накоплении соответствующего опыта) достаточно слабыми внешними воздействиями на входные потоки направлять обновляемую систему по желательному пути развития.
Автор: Зайнетдинов Р.И. - д-р техн. наук, проф. кафедры «Инновационные технологии» Московского государственного университета путей сообщения (МИИТ).
Список литературы:
- Зайнетдинов Р.И. Моделирование свойств инноваций на основе энтропийного, мультифрактального и вейвлетного анализа // Управление инновациями 2009: Материалы международной научно-практической конференции.– М.: ЛЕНАНД, 2009.
- Чесбро Г. Открытые инновации. –М.: Поколение, 2007.
- Пригожин И. Введение в термодинамику необратимых процессов. – М.: ИЛ, 1960.
- Zainetdinov R. Entropy Dynamics Associated with Self-Organization // Paradigms of Complexity. Fractals and Structures in the Science. – Singapore: World Scientific, 2000
- Николис Дж. Динамика иерархических систем: Эволюционное представление. – М.: Мир, 1989.
- Zainetdinov R.I. Dynamics of Informational Entropy Associated with Self-Organization Process in Open System // Chaos, Solitons & Fractals. Pergamon, 1999. – Vol. 10, № 9.
- Синергетика инноваций / О.С.Сухарев, С.В.Шманёв, А.М.Курьянов. – М.: Финансы и статистика; ИНФРА-М, 2011.
- Николис Г., Пригожин И. Познание сложного / Пер. с англ. – М.: Мир, 1990.